This is a continuation of an earlier post on deciphering Ruan Pethiyagoda’s N-Queens solution tweet, which you can check out here.
In the first post, we deciphered the meaning of numSolutions, cols, and done. This leaves us with poss, bit, leftDiagonal, and rightDiagonal.
The Diagonals
The two diagonal variables, leftDiagonal and rightDiagonal, don’t actually represent all the spaces along a given diagonal. Instead, they represent columns for the row we’re examining, which may already be under attack from a queen. If a queen is on the leftDiagonal of a given column for the row we’re examining, then leftDiagonal will have a 1 for that column. Unsurprisingly, the same goes for rightDiagonal.
So how does Ruan increment these variables? By using poss and bit.
poss
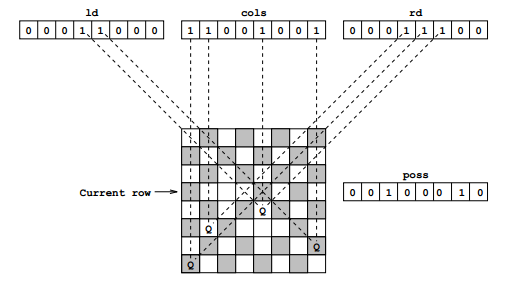
Ruan combines all the information stored in leftDiagonal, rightDiagonal, and cols into a single variable, poss. Remember, each of these three variables represents any “under attack” columns with a 1. By combining the three columns representations with bitwise OR operators, Ruan is left with a variable which contains a 1 for ANY column under attack. This variable is then inverted (with the ~ operator), so any columns which are NOT under attack are represented with a 1.
For example, with a 5x5 matrix with a Queen in the top-left cell, LD will be 00000, cols will be 10000, and RD will be 01000. poss, therefore, will be initially set to 11100, and then inverted to 00011, meaning we can only potentially add a queen on the second row in the last two spaces.
bit
This poss variable is then used by bit, which uses the properties of two’s complements to pick the rightmost of these open spaces. The fact that the algorithm picks the rightmost of these positions isn’t important; it would work equally well if the leftmost position was picked. The bit variable simply represents a single position where we want to place a queen.
Remaining Logic
After designating the column in which we want to place a piece (designated by bit), the algorithm still needs to step through to the next row. But how will we update the variables to reflect the fact that we’ve placed a piece?
Ruan simply calculates how the impact of placing that piece is going to affect LD, RD, and cols for the next row. bit, representing the piece to be added, is combined with each existing column representation of squares under attack. For diagonals, this “under attack” column representation is then shifted to the left/right by one bit, as the queen which attacks column B on a diagonal for row 2 will be attacking attacking different columns (C and A) when we advance to the next row.
Further reading
That’s all folks! If you’re interested in learning more, I highly recommend checking out the paper this algorithm came from, as well as a much cleaner Javascript implementation.